解非线性最小二乘问题
解决非线性最小二乘(非线性数据拟合)问题
语法
描述
非线性最小二乘求解器
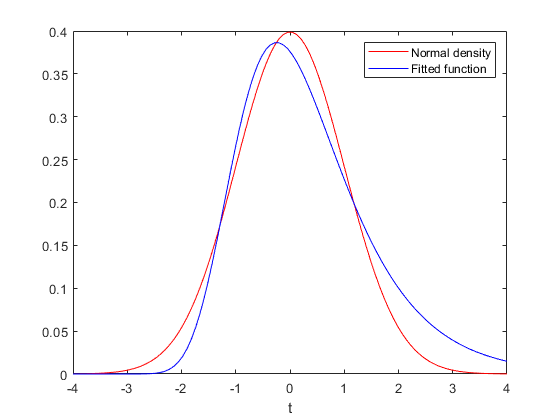
解决形式的非线性最小二乘曲线拟合问题
可选的下界和上界磅和乌兰巴托关于x.
x,磅和乌兰巴托可以是向量或矩阵;看见矩阵参数.
而不是计算价值
(平方和)解非线性最小二乘问题需要用户定义的函数来计算矢量价值函数
例子
输入参数
输出参数
限制
Levenberg-Marquardt算法不处理边界约束。
信任区域反射算法不解决未确定的系统;它要求等式的数量,即行维度F,至少与变量数量一样伟大。在未定的案件中,
解非线性最小二乘问题使用Levenberg-Marquardt算法。由于信任区域反射算法不处理欠定系统,而Levenberg-Marquardt不处理边界约束,因此同时具有这两种特征的问题不能用
解非线性最小二乘问题.解非线性最小二乘问题能直接用levenberg-marquardt算法。但是,该算法不接受约束约束。对于绑定约束的复杂问题,将变量拆分为真实和虚部,并使用trust-region-reflective算法。看到适合复杂的数据模型.信赖域反射法的预处理共轭梯度部分使用的预处理子计算形式JTJ(J为雅可比矩阵)。因此,一排J有许多非零,这会导致几乎稠密的乘积JTJ,可能导致大型问题的解决过程成本高昂。
如果组件x没有上部(或更低的)界限,
解非线性最小二乘问题首选的是乌兰巴托(或者磅)着手正(或者负而不是一个任意但非常大的正数(或负数的下界)。
您可以在中使用信赖域反射算法解非线性最小二乘问题,最小二乘拟合和FSOLVE.不计算雅可比矩阵的中小型问题享乐或者提供雅可比稀疏模式。(这也适用于使用铁铬镍铁合金或fminunc没有计算Hessian或提供Hessian稀疏模式。)中小型规模有多小?没有绝对答案,因为这取决于计算机系统配置中的虚拟内存量。
假设你的问题已经解决了M方程式N未知数。如果是命令J=稀疏(一(m,n))引起内存不足如果您的计算机出现错误,那么这肯定是一个太大的问题。如果它没有导致错误,那么问题可能仍然太大。您只能通过运行它并查看MATLAB是否在系统可用的虚拟内存量内运行才能找到答案。
算法
Levenberg-Marquardt和信任区域反射方法基于也使用的非线性最小二乘算法FSOLVE..
默认信任区域反光算法是子空间信任区域方法,基于内部反射牛顿方法[1]和[2].每次迭代涉及使用预处理共轭梯度(PCG)的方法的大线性系统的近似解。看到Trust-Region-Reflective最小二乘.
参考文献中描述了Levenberg-Marquardt方法[4],[5]和[6].看到Levenberg-Marquardt方法.
工具书类
[1] 科尔曼、T.F.和Y.Li。有界非线性极小化的内部信赖域方法SIAM优化学报,第6卷,1996年,第418-445页。
[2] 科尔曼、T.F.和Y.Li。“关于有界的大规模非线性极小化的反射牛顿法的收敛性。”数学规划,第67卷,第2期,1994年,189-224页。
[3] Dennis,J.E.JR.“非线性最小二乘”。数值分析的最新进展, D.雅各布斯,学术出版社,269-312页。
[4] Levenberg, K. <一种求解最小二乘某些问题的方法>。应用数学季刊2,1944年,第164-168页。
[5] Marquardt,D。“一种用于非线性参数的最小二乘估计的算法。”暹罗应用数学杂志,第11卷,1963年,第431-441页。
[6] Moré, J. J. < Levenberg-Marquardt算法:实现和理论>。数值分析,ed。G. A. Watson,数学讲义630,Springer Verlag,1977,PP。105-116。
[7] Moré, J. J., B. S. Garbow, K. E. Hillstrom。MINPACK 1用户指南.argonne国家实验室,Rept。ANL-80-74,980。
[8] Powell, M. J. D. <求解非线性代数方程组的Fortran子程序>。非线性代数方程的数值解法,P.Rabinowitz主编,第7章,1970年。